面元和球体元的几何构建和应用

面元和球体元的几何构建和应用

杨阳

川南幼儿师范高等专科学校 四川内江 642150

摘要：大学物理中的球坐标中的面元与体元公式一直是相关专科院校大学生学习的难点。而各类教科书只给出体元和面元公式的结果，忽略过程。导致学生只能死记硬背，不方便与理解和记忆。本文通过微积分思想分别对圆形和球体进行面元、体元的构建。透过其构建思想引申到分析圆形的面积公式和周长公式之间的导数关系，以及球体积公式与球表面积公式之间的导数关系。并简要介绍其在物理教学方面的应用。相关结论可为提高大学物理教学质量提供参考和帮助。

关键词：面元；体元；导数关系。

球坐标中的面元与体元公式一直是大学物理教学中的难点。然而在大多数院校的物理教学中，基本对球坐标、柱坐标下的体元表达式都是直接引用，并未做详细推导。本文就球坐标、柱坐标系下的面元与体元表达式进行详细探讨，并通过面元与体元，推导表出球面积和球体积的公式。数形结合是数学物理问题中，研究坐标系中的问题，必然要结合具体图形分析。

一、极坐标下的面元

如图1所示，对于平面上的一个实心圆(仅显示了四分之一部分)，将其圆心设为坐标原点O，以水平向右为正方向建立极坐标系，x为极轴。在实心圆中任取一点P，假设OP长度为r，则P点的位置矢量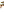 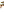可以表示为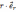 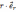，即图1中的有向线段(箭头)OP。为了建立面元，我们将OP沿角方向逆时针旋转一个非常微小的角度dθ，使得dθ趋近于0，得到OQ，以及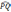 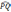这一段微小圆弧，由几何关系可知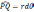 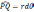，同样满足 。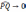

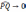接下来，过P点，沿有向线段OP所指的半径方向作dr，使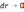 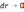。同理，过OQ也得到相应dr。由于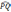 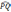无穷小，可以将其近似看作一条直线，且该直线与dr相互垂直。而两个dr的箭头处所连弧线同样可以近似看作直线，且与两dr垂直，与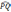 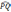平行。由几何关系，其长度为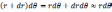 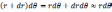，drdθ是rdθ的高阶无穷小，故约去。

经上述操作，在图1中P点处出现了一个面积趋近于无穷小的面元。该面元可以近似看作是矩形，面积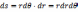 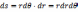。由于P点是任意选取的，因此，P点可以随着不同的r和不同的θ出现在圆的任何位置，这也意味着该矩形面元可以连续分布在整个圆中。为了验证以上所述，我们对该连续分布的面元进行求和，也就是积分，就得到圆的面积：

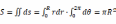
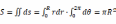(1)

所以，圆的面积公式，可以通过无穷多个无穷小矩形面积来近似求得。

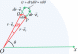
图1. 圆形的面元的建立 图2.圆看作为圆环的叠加 图3.探究面元对质点的引力

二、面元思想的应用

(一)解释圆面积公式与圆周长公式之间的一阶导数关系

圆的面积公式πr²对半径r求一阶导数，恰好等于圆周长公式2πr，这究竟是巧合还是其背后确实蕴含了某种原理？我们可以将一个圆看作是不同半径的圆环叠加，如图2所示。r为任意圆环的半径，无穷小的dr为圆环的宽度。因此我们可以在圆上取出无穷多不同半径r的无穷小宽度的圆环。对于半径为r的圆环的面积，我们假想将圆环某处沿半径的方向切断，将圆环拉开。同时，考虑到dr趋近于0，圆环拉开后可以看作是一个矩形，圆环周长2πr是其长，dr为其宽，其面积可以表示为ds=2πrdr。将不同半径的圆环面积求和，即

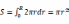
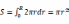(2)

由式(2)可看出，圆的面积其实就是圆周长公式沿半径方向的路径积分。其对半径的一阶导数就是圆周长。

(二)求解圆盘(柱)以中心轴定轴转动的转动惯量

对于质量连续且均匀分布的圆盘(柱)，如图2所示，假设其总质量为M，半径为R，对圆上选择任意一点，并取面元，则任意面元质量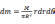 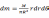。当圆盘(柱)绕其过圆心的对称轴做定轴转动时，其转动惯量为 。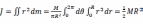

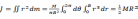(三)证明呈平方反比的力的问题中均匀球体可以当作质量集中在其球心的质点

以万有引力的计算为例，研究半径为R的质量均匀分布的球体和距离球心O为d的质量为m的质点P之间的万有引力大小。根据对称性，我们只需要选取过OP连线的半个面，在这个面上取无穷小的面元，如图3所示。取任意r，θ处的无穷小面元，尽管图中将面元画的很大，但实际因为其无穷小所以可以将其当作质点处理，令其面密度为σ，则其质量du=σrdrdθ 。面元对质点的引力大小dF=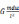 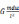，其中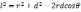 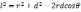，为面元到质点的距离。根据对称性，上下半圆相对位置的面元对质点的万有引力的竖直方向的分力相互抵消，水平方向叠加。于是整个圆的对质点的万有引力为 = 。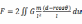

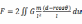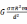
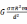与两个相距为d的质点的引力公式相同。可见，对于质量均匀分布的圆形，其对某质点的引力等效于其质量全部集中于其圆心的质点的引力，由于球体可看成是由无数个这种圆形构成，根据对称性，球体对某质点的引力也等效于其质量全部集中于其球心的质点的引力。

三、球、柱坐标下的体元

与空间直角坐标系下的体元dV=dxdydz不同，球坐标系下的体元的建立无法直接通过drdθdφ来得到，而应将θ，φ这样的角量转化为长度量。如图4，在距离原点O为r

处有一点P，OP与z轴夹角为θ，延OP方向作一无穷小长度dr，作为体元的一条边。接下来，让OP沿着θ增大的方向，圆心O端不变，使OP转动无穷小的角度dθ，P点划出的轨迹成为体元的另一条曲边，长度为rdθ。OP在xoy平面上的投影为rsinθ。该投影与x轴夹角为φ。将该投影平移至P点，成为线段QP。以O为固定点，使OP顺着φ增大的方向转动无穷小的角度dφ，此时P点就划出了长度为rsinθdφ的第三条曲边。这三条曲边在其连接处P点相互垂直，同理，根据几何对称作出相应虚线，构成图3中的体元。由于dr，rdθ，rsinθdφ均为无穷小，可近似当作直线处理。所以可通过长方体的体积公式来求该体元的体积，即 。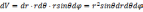

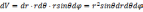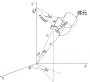
图4.球体的体元 图5.柱体的体元 图6.球看作球壳的叠加

经过上述操作，P点处就建立起了一个体积为dV的体元，由于P点是在球体内任意选取的，同时体元在球体内连续分布。因此，整个球体可以看作由是无数个连续分布的体元所构成。因此，球的体积

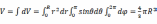
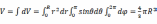(3)

这里要说明，在这个积分中，θ的变化范围只需0到π，φ的变化范围需0到2π，即可积分到整个球体。

将面元和体元的构建方法整合起来，就可以构建柱坐标下的体元。如图5所示。对于一个高为H的圆柱体。以其底面的圆心O为坐标原点，建立如图所示的空间直角坐标系，其中，圆柱的轴为z轴。在z轴上任取一点P，OP长度为z，z的取值范围为0到H 。过P点，沿着Z轴取一段无穷小的线段PQ，长度dz，同时过P点，沿半径方向作与X轴夹角为φ的虚线段，其长度为r，取值范围为0到R 。接下来该线段顺着φ增大的方向偏移一个无穷小的角度dφ，其划出的弧长即为rdφ 。接下来，将两个r虚线段各自沿着半径向外延伸一个无穷小的长度dr，则这个长度为r+dr的虚线段末端构成的圆弧长为(r+dr)dφ≈ rdφ，类似于这里同样是忽略掉高阶无穷小项drdφ 。由于圆弧长均rdφ与dr均为无穷小，且相互垂直，因此可将其体元近似看作为长方体，则该体元体积表达式为dV=rdrdφdz 。对其进行积分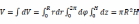 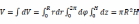，与柱体体积计算公式一致。

四、体元思想的应用

(一)解释球的体积公式与球表面积之间的一阶导数关系

与圆的面积和周长之间的关系类似。对于球体来说，其表面积公式也等于其体积公式对半径r的一阶导数。同样，这也不是巧合。在一个半径为R的球体内部，以球心O做起点，画出一个半径为r的球，(r<R)，如图6中的虚线球。接着在这个小球外，沿着半径向外取一个无穷小的长度dr，那么半径为r的小球的球面与半径为r+dr的小球的球面共同构成了一个厚度为dr的球壳。由于dr趋近于0，该球壳可近似展开为一个无限薄，即高为dr的立方体，其体积dV=4πr²dr。由于r的取值范围是0到R，每一个r都可以作出一个厚度dr的球壳，同时这些球壳在球体内连续分布。于是可以将半径为R的整个大球看作由无穷多个厚度为dr的球壳构成。则半径为R的大球体积为无穷多个厚度是dr的球壳体积之和，即

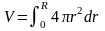(4)

由式(3)可以看出，球的体积其实就是球表面积公式沿半径方向的路径积分。因此球体积公式对半径的一阶导数就是球表面积。

(二)求解与类似f(r,θ,φ)的物理问题

对于圆柱形157组件的压力轻水冷堆，其堆芯核燃料组件会根据核燃料富集度进行不同梯度放置。而对于堆芯核燃料分布呈球对称的球形堆，由于堆芯入口和堆芯出口温度差异巨大，导致在某平衡态下整个堆芯的冷却剂密度分布函数f(r,θ,φ)=φ/(r·sinθ)。则当前状态下堆芯中子总量N= 。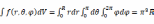

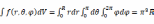五、总结

本文从微分几何的角度分别介绍了圆形、柱体和球体的体元的构建思路方法，并精选了经典的物理学问题来详解这些知识的用法。其中对圆周长公式与面积公式之间的联系、球表面积公式与球体积公式之间的联系进行了剖析。

参考文献：

[1]Yang Yang, et al. Introducing time in derivation of the scaling factor for MCNP criticality calculations[J], Annals of Nuclear Energy, Volume 87, Part 2, 2016, Pages 385-387

[2]杨阳; 不同铀浓度对混合燃料超热熔盐堆的增殖率及石墨寿命的影响[J]; 科技创新与应用; 2015年24期

作者简介: 杨阳(1989-)，男，助讲，硕士，主要从事物理课及计算机课程的辅助教学。

基金项目：川南幼儿师范高等专科学校青年课题《科学教学模型的可视化研究》(编号：CNYZ2019C10)。