梅县区高级中学 广东省 梅州市 514000
摘要:数学思想是解决数学问题的灵魂,在数学教学中注意对函数与方程、化归与转化、分类讨论、数形结合、极限等数学思想的渗透,有利于提高学生的解题能力,从而提高整体素质。本文就上述数学思想在解题中的渗透提出自己的看法。
关键词: 渗透; 思想; 优化; 途径
数学思想方法是处理数学问题的指导思想和基本策略,是数学的灵魂和精髓。只有用数学思想武装起来的学生在解决数学问题时才能有远见和洞察力,才能形成科学的世界观和方法论。中学数学思想是指渗透在中学数学知识和方法中具有普遍而强有力适应性的观点和认识。教师应结合具体的教材在传授知识的同时挖掘教材中的数学思想,注重数学思想的渗透,有利于优化解题途径,提高解题能力,进而提高数学教学效率。本文就数学教学解题中如何渗透函数与方程、化归与转化、分类讨论、数形结合以及极限等数学思想,谈谈自己的看法。
一、函数与方程的思想
函数思想是数学中的重要思想,用运动、变化的观点分析、处理变量与变量之间的关系是函数的精髓。在解题中如能运用函数思想合理选择函数关系式,就能使解题思路自然流畅。例如2000年全国高考题中的一道题:
设![]() 为等差数列,
为等差数列,![]() 为数列
为数列![]() 的前n项和,已知
的前n项和,已知![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前n项和,求
的前n项和,求![]() 。
。
该题若先求![]() 的首项和公差,进而求出
的首项和公差,进而求出![]() ,最后求出
,最后求出![]() 。这种解法容易想到,但运算量大。在教学中,若启发学生从函数观点出发,把数列看作一个定义域为非零自然数集N或它的有限子集{1,2,…,n}的函数。对于公差不为0的等差数列,它的通项是关于n的一次函数,对应点均匀分布在一条直线上,它的前n项和是关于n的无常数项的二次函数,故而
。这种解法容易想到,但运算量大。在教学中,若启发学生从函数观点出发,把数列看作一个定义域为非零自然数集N或它的有限子集{1,2,…,n}的函数。对于公差不为0的等差数列,它的通项是关于n的一次函数,对应点均匀分布在一条直线上,它的前n项和是关于n的无常数项的二次函数,故而![]() 也是关于n的一次函数,不妨设
也是关于n的一次函数,不妨设![]() ,由已知条件列出关于p、q的二元一次方程组,很快就能求出p、q的值,进而求得前n项和
,由已知条件列出关于p、q的二元一次方程组,很快就能求出p、q的值,进而求得前n项和![]() .
.
这种解法体现了函数思想在解题中的地位和作用。
关于方程思想的渗透也类似,比如94年的一道高考题:
设![]() ,求
,求![]() 。
。
该题最为直接的解法是先求出![]() ,然后求
,然后求![]() 。但这样计算显得麻烦。若能注意到
。但这样计算显得麻烦。若能注意到![]() 与
与![]() 间的关系,求
间的关系,求![]() 的值,实际上就是求方程
的值,实际上就是求方程![]() 的解,令
的解,令![]() ,解得
,解得![]() ,于是
,于是![]() 。通过此例让学生领会到:可把函数解析式看作一个方程,通过对方程的研究使问题获解。
。通过此例让学生领会到:可把函数解析式看作一个方程,通过对方程的研究使问题获解。
二、化归与转化的思想
数学中的化归,是把待解决的问题转化为一类已经解决或比较容易解决的问题,最终使原问题获解。它是数学中最典型、最基本和最富有数学特色的方法之一。美籍匈牙利著名数学家玻利亚说:解数学题的关键在于转化。要实现转化,关键在于寻求正确的化归、途径和选择恰当的化归方法。比如,1995年高考题:
已知椭圆![]() ,直线L:
,直线L:![]() ,P是L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足
,P是L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足![]() ,当点P在L上移动时,求点Q的轨迹方程。
,当点P在L上移动时,求点Q的轨迹方程。
本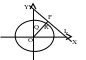 题难点在于轨迹条件中,
题难点在于轨迹条件中,![]() 是三条线段成等比数列的形式。实际上,化解这个难点的好方法是来自解析几何的一个基本思想和基本方法——降低维数,化二维问题为一维问题。
是三条线段成等比数列的形式。实际上,化解这个难点的好方法是来自解析几何的一个基本思想和基本方法——降低维数,化二维问题为一维问题。
设点Q、R、P的坐标分别为![]() ,
,![]() ,(
,(![]() )则把关系式
)则把关系式![]() “投影”到x轴上得
“投影”到x轴上得![]() ,又设OP的方程为
,又设OP的方程为![]() ,因为P是L与OP的交点
,因为P是L与OP的交点
所以![]()
![]()
![]()
同样,因为R是椭圆与OP的交点
所以![]()
![]()
![]()
又因为![]()
![]()
![]() ①
①
由![]()
![]()
![]() ②
②
由①②消去K并整理得点Q的轨迹方程为:![]()
由此例可见,在解题过程中,把高维问题低维化,选择恰当的化归途径对问题进行转化,能有效地促进问题的解决。
三、分类讨论的思想
分类讨论是重要的数学思想,又是一种重要的解题策略。许多数学问题很难从整体上去解决,但只要将其划分为所包含的各个局部问题就可以逐个解决。分类讨论的思想实质上就是各个击破的策略,它对培养学生思维的严谨性有着极其重要的作用。
例如:3个实数![]() 适当排列,分别取常用对数后构成公差为1的等差数列,求此时
适当排列,分别取常用对数后构成公差为1的等差数列,求此时![]() 的值。
的值。
分析:此题关键是3个数以怎样的顺序构成等差数列?由公差为1可知,此等差数列一定是递增的,所以需判断这3个数的大小关系,从而减少分类次数。
解:设![]()
由题意知:![]() >0,
>0,![]() >0,
>0,![]() >0
>0
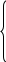
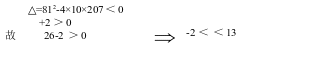
考虑差 ![]()
![]()
因为 △1=802-4×10×205<0
△2=832-4×10×181<0
所以 ![]() >
>![]() ,
,![]() >
>![]()
又 ![]() -
-![]() =3(
=3(![]() -8)
-8)
① 当 ![]() =8时,
=8时,![]() =
=![]() (不合题意)
(不合题意)
② 当 -2<![]() <8时,
<8时,![]() <
<![]() ,此时有
,此时有![]() >
>![]() >
>![]()
![]() 构成公差为1的等差数列
构成公差为1的等差数列
即![]()
所以![]()
即![]() 解得
解得![]()
③ 当 8<![]() <13,
<13,![]() >
>![]() ,此时
,此时![]() >
>![]() >
>![]()
![]() 构成公差为1的等差数列
构成公差为1的等差数列
即![]()
所以 ![]()
即![]() 此方程组无解,即
此方程组无解,即![]() 不存在
不存在
综合①、②、③知![]()
从上例可看出,分类讨论时要善于观察分析,善于把握事物的特性和规律,把握分类的标准,做到正确分类,可优化解题途径。
四、数形结合的思想
数学是研究现实世界的数量关系和空间形式的一门科学,数与形有着密切的联系。华罗庚有句名言:数缺形时少直观,形缺数时难入微。指的就是数与形结合有助于问题的解决。
例如(1985年全国高考题)已知![]() ,
,![]() ,
,![]() ,
,![]() 是平面
是平面![]() 内点的集合,讨论是否存在实数
内点的集合,讨论是否存在实数![]() ,
,![]() ,使得①
,使得①![]() ;②
;②![]() 同时成立。
同时成立。
解:假设![]() ,
,![]() 存在,由条件①有
存在,由条件①有![]() (1)
(1)
由条件②有![]() (2)
(2)
设原点到直线![]() :
:![]() 的距离为
的距离为![]() ,则
,则
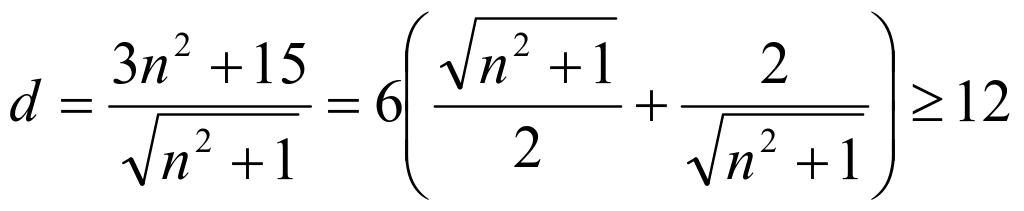
当且仅当![]() ,即
,即![]() ,
,![]() 时,等号成立,而
时,等号成立,而![]() ,这不可能。
,这不可能。
故![]() >12
>12
由(1)式知点![]() 在直线
在直线![]() 上,所以
上,所以![]() >12,这与(2)式
>12,这与(2)式![]() 矛盾。
矛盾。
所以不存在实数![]() ,
,![]() ,使得①、②同时成立。
,使得①、②同时成立。
在此题的解法中,我们运用数形结合的思想,充分挖掘数的特征与形的结构之间的关系,以数构形,以形示数,使抽象的概念和数量关系直观化、形象化,寻觅出新的解题思路,为问题的解决提供了新的途径。
五、极限思想
极限是高中数学中的重要的概念,也是高考必考的内容之一,在高中数学教学中大家往往只把注意力放在求某一个式子的极限值或用定义证明极限等问题上,而对极限思想的应用还未引起足够的重视。但不少数学题用一般方法解答十分繁琐,而应用极限思想来处理却能体现数学的美妙之处。
例如:过椭圆![]() 上一点
上一点![]() 的两条弦PA、PB分别与长轴交于M、N两点,若
的两条弦PA、PB分别与长轴交于M、N两点,若![]() ,求直线AB的斜率。
,求直线AB的斜率。
解法1:设PA所在直线方程为![]() (t为参数,α为PA的倾斜角) 代入椭圆方程,得
(t为参数,α为PA的倾斜角) 代入椭圆方程,得 ![]()
故得A对应的参数值 ![]()
由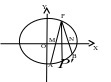
![]() 知,PB的倾斜角为
知,PB的倾斜角为![]() ,与上式比较,
,与上式比较,
很容易得到点B对应的参数值为![]()
![]()
所以![]()
解法2:先求得点P关于X轴的对称点![]() 的坐标为
的坐标为![]() ,因为过椭圆
,因为过椭圆![]() 上一点
上一点![]() 的切线方程为
的切线方程为![]() ,故过点
,故过点![]() 的切线方程为
的切线方程为![]() 。
。
从而可得其斜率为![]() ,故所求直线AB的斜率即为
,故所求直线AB的斜率即为![]() 。
。
在此题中,对条件![]() 一般可以理解为无论点A、B在椭圆上怎样运动,△PMN均保持以点P为顶点的等腰三角形。当A、B重合时割线AB此时就成为切线,把A、B重合后的点设为
一般可以理解为无论点A、B在椭圆上怎样运动,△PMN均保持以点P为顶点的等腰三角形。当A、B重合时割线AB此时就成为切线,把A、B重合后的点设为![]() ,则点
,则点![]() 与点P关于
与点P关于![]() 轴对称,由极限思想可知过
轴对称,由极限思想可知过![]() 处的切线与割线AB是平行的,故而求得的切线的斜率就是割线的斜率,解法2比解法1简洁而又明快。
处的切线与割线AB是平行的,故而求得的切线的斜率就是割线的斜率,解法2比解法1简洁而又明快。
总之,教师在数学教学中应对一些重要的数学思想精心挖掘,系统归纳,积极渗透,不但可以优化解题途径,提高数学能力,而且能促进学生综合素质的全面发展,达到深化数学素质教育的目的。
参考文献:
1、李翼忠 中学数学方法论 北京、高等教育出版社 1986
2、丁赛军 数列中的数学思想 高中数学教与学 2003.11
3、李春辉 用数学思想方法求解探索性问题 数学教学通讯 2000.4
6