多中点几何问题的分析思考规律

多中点几何问题的分析思考规律

郭忠兰

宜良县第五中学 云南昆明 652100

[摘要]: 对于多中点的几何问题可运用中位线的定理来进行证明或计算。但要在何处取出中点,使两个中点所连的线段巧妙地构成一个三角形或梯形的中位线,这个问题还需要我们进一步地研究.

[关键词]: 中点 ;中位线; 平行;相等;

[abstract]:we can use The median line theorem to calculate or

proof the Problems of more than the midpoint.But we shuld findout where to Retrieve,when we connected two midpoints

ingeniously,which can form the median line about Triangular and trapezoidal. So this issue still needs further study.

[key words]: Midpoint median line Parallel Equivalence

目录

1﹑ 多中点几何问题的定义--------------------------------3

2﹑学生学习多中点几何问题时遇到的困难------------------------3

3﹑ 解多中点几何问题的必备知识-------------------------3

4﹑ 多中点几何问题的分类解题策略------------------------3

4．1，连结中点，直接解题--------------------------3-6

4．2，作辅助线，巧妙解题--------------------------6-9

参考文献----------------------------------10

1. 多中点几何问题的定义

对于几何问题的条件或结论里出现了两个或两个以上的中点的几何问题称为多中点几何问题。

2．学生学习多中点几何问题时遇到的困难

学生叙述不清楚，说不清理由，对逻辑推理的证明过程几乎不会写，大多数学生尤其不知道要在什么地方取中点，连中线，从而能更容易地解决问题。

3．解多中点几何问题的必备知识

在平时的解题中,我们经常遇到“中点”,那么我们如何运用中点位置的特殊性解题呢?首先我们了解一下与中点有关的几个定理:

①等腰三角形底边上的中线、高与顶角的平分线互相重合;

②直角三角形斜边上的中线等于斜边的一半;

③三角形的中位线平行于第三边,并且等于第三边的一半;梯形的中位线平行于两底,并且等于两底之和的一半;

④经过三角形一边中点与另一边平行的直线必平分第三边;经过梯形一腰中点与底边平行的直线,必平分另一腰.

4．多中点几何问题的分类解题策略

4．1﹑连结中点, 直接解题

如果有中点的线段有公共端点,则只要连其两个中点,则中点的连线就是某一个三角形的中位线.另外,若在一个三角形中,有中位线而无底边,则要把底边添上.

例1﹑已知如图（1），以△ABC的边AB. AC为边分别向外作等边△ABD和等边△ACE, F﹑G

H分别为线段BC﹑BD﹑CE的中点,求证FG=FH

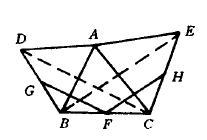
图（1）

分析:如图一,G﹑F﹑H分别为BD﹑BC﹑CE的中点,连结BF﹑FH使之分别成为△BDC，△BCE的中位线。注意在三角形中，有中位线，而无底边时，则应把底边添上。因此我们要连结底边DC﹑BE.欲证FG=FH,只要证CD=BE,欲证CD=BE，只要证△ADC≌△ABE

证明：连结GF﹑FH,并连结DC﹑BE

∵G﹑F﹑H分别为BD﹑BC﹑CE的中点

∴GF DC FH BE

又∵△ABD和△ACE均为等边三角形

∴AD=AB AC=AE

又∵∠DAC=∠EAB

∴△ACD≌△AEB

∴DC=BE

∴FG=FH

例2．已知如图（4），在△ABC中，BD﹑CE分别是AC﹑AB边上的中线，BD与CE相交于点O,F﹑G分别是OB﹑OC的中点，求证：EF=DG.

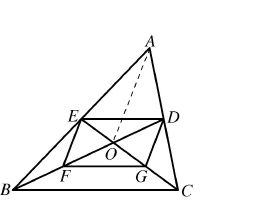
图（4）

分析：此题的条件和结论中出现了4个中点，属于多中点几何问题。由E﹑F﹑G﹑D分别为AB﹑OB﹑OC﹑AC的中点，连结EF﹑EG﹑GD﹑DE﹑AO, 可得EF= AO, DG= Ao, 由此得EF=DG

证明：连结EF﹑EG﹑GO﹑DG﹑AO

∴E﹑F﹑G﹑D分别是AB﹑OB﹑OC﹑AC的中点

∴EF= AO DG= AO

∴EF=DG

4．2.作辅助线，巧妙解题

如果有中点的线段无公共端点或重叠在一条线上，而中点的连线不是中位线，这时需要增加中点，且应增加和已知有中点的线段有公共端点的线段的中点。

例3 ．如图五，在△ABC中，点D﹑E分别在AB﹑AC上，且DB=EC,点M﹑N分别为BE﹑CD的中点，直线MN交AB于p点，交AC于Q点，求证：AP=AQ

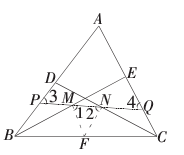
图（5）

分析：此题的条件和结论中出现了两个中点，属于多中点几何问题。但该题的中点的连线MN并不是中位线，此时需要增加和已知中点的线段BE与DC有交点的线段BC的中点F,连结 MF﹑NF,由MF EC , NF BD， 又因BD=EC,故MF=NF , ∠1=∠2,

∠2=∠3, ∠1=∠4,所以∠3=∠4,即有AP=AQ

证明：取BC的中点F, 连结MF﹑NF

∵M﹑N﹑F分别为BE﹑DC﹑BC的中点，

∴MF EC, NF BD

又∵DB=EC

∴MF=NF

∴∠1=∠2

又∵∠2=∠3, ∠1=∠4

∴∠3=∠4

即AP=AQ

例4．如图六，四边形 ABCD的对角线AC与BD相交于点 O,且AC=BD，M ﹑N分别为AB﹑CD的中点，MN分别交BD﹑AC于E﹑F,求证：OE=OF

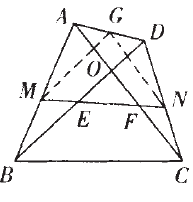图（6）

分析：本题的条件和结论中出现了两个中点，但当连结起中点M﹑N时, 但 MN并非是中位线。这时，需要增加中点，即取AD的中点为G，连结MG﹑NG，由中位线定理有MG BD,

GN AC,又由于AC=BD，即有MG=NG,从而进一步有∠GMN=∠GNM，又因∠GMN=∠DEN， ∠GNM=∠AFM，所以∠DEN=∠AFM，从而有OE=OF

证明：取AD的中点G,并连结MG﹑GN

∵M﹑N分别是AB﹑CD的中点

∴MG BD, GN AC

又∵AC=BD

∴MG=NG且∠GMN=∠GNM，∠GMN=∠DEN，∠GNM=∠AFM

∴∠DEN=∠AFM

∴OE=OF

上述几个例子，通过直接连结中点或巧妙地借助添加辅助线后，利用 三 角 形 的 中 位 线 ，既 能 把 线段 进 行转 移，又 可 以将 角进 行平 移 ，达 到 “移 动位 置 ，集 中条 件 ”的 目的，便可以使得看似没有好方法解决的几何问题迎刃而解。

同学们在遇到多中点问题时，要灵活运用上述思想方法，并在自己的练习过程中不断地归纳总结，以便能使自己的几何证题能力得到进一步的提高，从而培养自己对数学学习的浓厚兴趣。

[1] 吴友智. 巧用平移法解多中点问题[J]. 同学少年 , 2005,(Z1)

[2] 马根泉. 中点问题的一种处理方法[J]. 数学教学研究 , 2002,(11)

[3] 胡立鸣. 中点问题初探[J]. 濮阳教育学院学报 , 1996,(02)

[4] 陈绩馨. 浅谈平面几何辅助线的作用及常用方法[J]. 闽江学院学报 , 1996,(01) .

[5] 蔡进添. 初中几何学习的障碍分析及其对策[J]. 数学教学研究 , 1996,(01) .

[6] 黄家礼. 中位线定理及其推广[J]. 中学数学 , 1986,(06)

[7] 赵春光. “三角形中位线”说课设计[J]. 内蒙古教育 , 2004,(03)

[8] 刘秀华. 巧用三角形中位线定理解题[J]. 黑河教育 , 2003,(04)

[9] 赵春祥. 三角形、梯形的中位线典型问题解析[J]. 考试(中考版) , 2006,(09)

[10] 赵建勋. 三角形中位线定理的活用[J]. 中学生理科月刊 , 1995,(05)

参考文献

1. 窦安庆 《怎样解含中点的几何问题》 [J] 初中数学教与学，2006,(07)

第19—20页。

2．董开福.《中学数学教材分析》 [J]， 云南教育出版社，1999年版，第498—503页

3．吴友智. 《巧用平移法解多中点问题》 [J]， 同学少年 , 2005,(Z1) 第47页

4． 赵春祥. 《三角形、梯形的中位线定理的应用》[J], 中学生理科月刊2006,(07) 第26-27页

5．何建凯．《中点在解题中的运用例谈》[J],时代数学学习（八年级）2006，（06） 第11—13页

6．赵建勋． 《三角形中位线定理的活用》[J],中学生理科月刊1995，（05）

第19-23页

致谢

在论文的撰写过程中，从论文的选题到答辩的整个过程中都是在李嘉元教授的悉心指导下完成的。尤其，是在我写论文出现疑难问题时，李老师更是不辞劳苦尽心尽力地帮我解决。正是在李老师不遗余力的指导下，我才能顺利地，按质按量地完成了论文的撰写。在此，我对于老师们给以的指导和帮助表示衷心的感谢。再次，谢谢您们！

7